Inst. Automatismos

Mini-Maxi-términos

Si tenemos una variable binaria en su forma normal (x) y en su complemento (x’), ahora tenemos 2 variables x y y combinadas con una operación AND, entonces tenemos estas 4 posibles combinaciones: x’y’, x’y, xy’ y xy. Cada uno de estos términos se llaman «mini-términos». Si tenemos n variables se pueden formar 2ⁿ  diferentes mini-términos. Los números binarios de 0 a 2ⁿ – 1 se listan bajo las n variables con cada variable tildada, si el bit correspondiente al numero es 0 y si no esta tildada a 1, es decir si la variable esta tildada corresponde a 0 de lo contrario a 1.

Para los maxi-términos las n variables forman un termino OR, con cada variable tildada o no tildada, darán 2ⁿ combinaciones posibles de maxi-términos. Cada maxi-término se obtiene de un término OR de n variables con cada variable no tildada si el correspondiente bit es 0 y tildada si es 1.

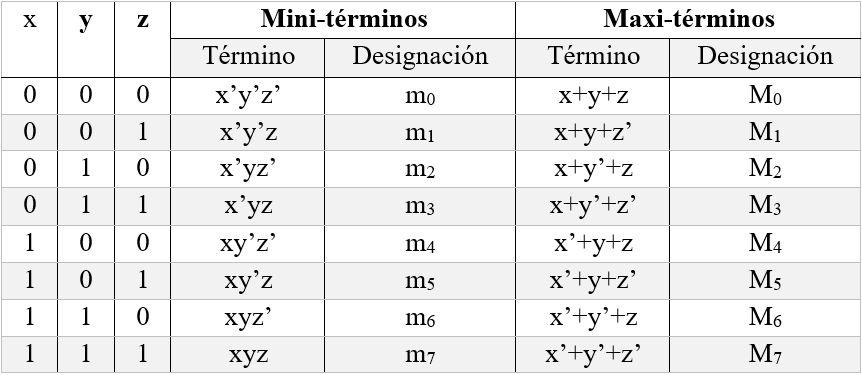
La siguiente Tabla es un ejemplo de los mini y maxi-términos para 3 variables.

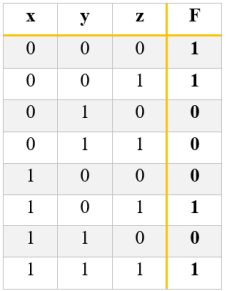
Para expresar la función F en mini-términos tomamos donde la función sea 1 y unimos los mini-términos con sumas(sumas de productos):Supongamos la siguiente función F dada a partir de la siguiente tabla

F= m₀ + m₁ + m₅ + m₇ = x’y’z’+ x’y’z + xy’z + xyz

F(x,y,z)= ∑ (0,1,5,7)

O bien se toman los ceros, pero no tendríamos a F, en su lugar tendríamos a F’

F’= m₂ + m₃ + m₄ + m₆ = x’yz’+ x’yz + xy’z’ + xyz’

F(x,y,z)= ∑ (2,3,4,6)

Ahora para obtener F en maxi-términos tomamos donde la función sea cero y unimos los maxi-términos con productos(producto de sumas):

F= M_2*M_3*M_4*M₆ = (x+y’+z)( x+y’+z’)( x’+y+z)(x’+y’+z)

F(x,y,z)= ∏ (2,3,4,6)

La otra manera es con unos, pero al igual que con los mini-términos obtendríamos F’

F’= M_0*M_1*M_5*M₇= (x+y+z)( x+y+z’)( x’+y+z’)(x’+y’+z’)

F'(x,y,z)= ∏ (0,1,5,7)

Ahora para reducir la función debemos aplicar Álgebra de Boole, pero sale muy largo así que optimizamos con mapas de Karnaugh.

Mapas de Karnaugh

Es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.

Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, las cuales saldrían muy extensas simplemente usando mini o maxiterminos para representar la función.

El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2^N filas, el mapa K correspondiente debe poseer también 2^N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo elcódigo Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que toma la función en cada fila.

La imagen explica el funcionamiento de un mapa de Karnaugh para una función de de 4 variables de entrada y una función de salida, en el mapa se muestra su correcta ubicación de posiciones para cada uno de los mini-términos, donde A es el mas significativo y va decayendo su valor regido por el orden alfabético hasta llegar a D que toma la posición menos significativa.

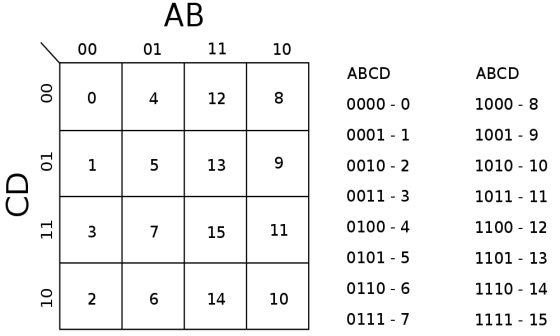
La función F que determina los números pares de los primeros 8 números binarios esta compuesta por 3 variables de entrada(A,B,C), F se define en la siguiente tabla:

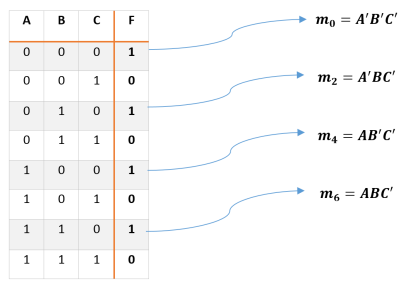
Como podemos observar en la tabla la funcion se puede escribir como la suma de los mimiterminos 0,2,4,6 de la sIguiente forma:

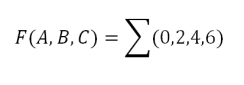
Reemplazándolos por miniterminos y operando con Álgebra de Boole nos queda:

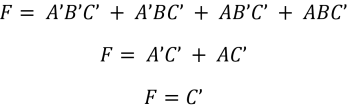
Ahora lo hacemos por Mapas de Karnaugh

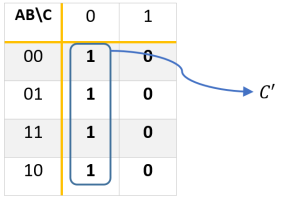
Imagen 1.Mapa de Karnaugh de F

En la Imagen 1 se ve como varia AB con respecto a los términos encerrados en el conjunto azul, C no varia puesto que se queda fija en 0, como AB varían no los tomamos, C no varia pero es 0  entonces es C’, si se mantuviera en 1 entonces seria C.

En el mapa solo se observa un conjunto lo cual indica que la función de salida es la que sea producida por el conjunto. Si hubieran dos o mas conjuntos o agrupaciones tomaríamos la función final como la suma de cada una de las funciones de cada conjunto.

Como se observa en la Imagen 1 con respecto a los miniterminos, el mapa nos reduce considerablemente el trabajo de aplicar Álgebra de Boole.

Términos No-Importa

En algunos casos de la practica vamos a encontrarnos que no todos los 2ⁿ mini o maxiterminos posibles son aplicables en algunos casos. A estos términos que no son aplicables les llamamos términos no importa.

Los términos no importa se representan en mapas con una x y se pueden tomar en el mapa de Karnaugh con un uno o un cero, cualquiera de los dos para simplificar mas la función de salida.

Ejemplo:

Se requiere señalar los múltiplos de tres de  los primeros diez números BCD, reducir la expresión de salida con mapas de Karnaugh

• Primero hacemos la tabla de verdad de este codigo

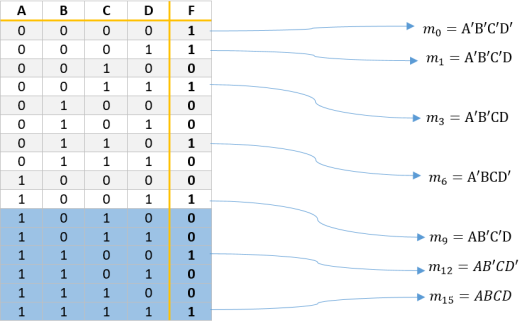
En la tabla hay unos términos en azul, estos términos se pueden clasificar en términos no-importa ya que el código BCD va hasta el bit 9-«1001», así que estos posibles estados de entrada son no-importa, ahora los reemplazamos en la tabla y hacemos su mapa de Karnaugh correspondiente.

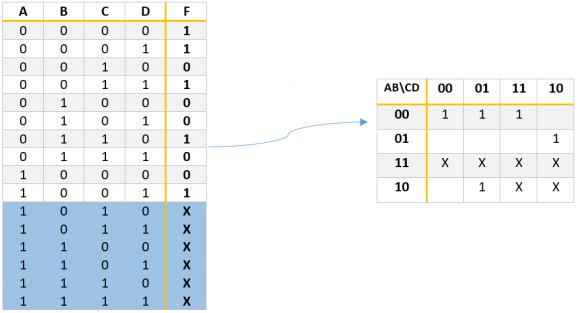
Ahora tomamos los términos no importa como 1 para simplificar la función «F», hacemos grupos de términos con los no-importa y simplificamos la función.

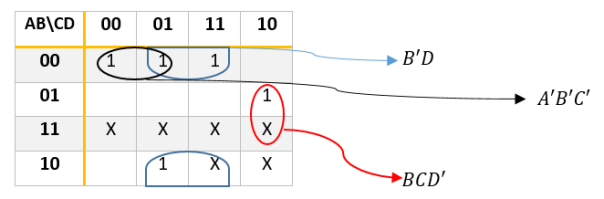
• La función del conjunto azul se produce por que se observa que A varia durante su conjunto por consiguiente no lo tomamos, B no varia pero es 0 constante asi que es B’, C varia durante el conjunto azul entonces no lo tomamos, D no varia y se mantiene en uno asi que es D, obtenemos por consiguiente a B’D como función de ese conjunto.
• La función del conjunto negro se produce al observar que D varia por tanto no se toma, A,B Y C no varían y se mantienen contantes como 0 así que obtenemos como función del conjunto rojo a A’B’C’.
• En el caso del conjunto rojo solo A no varia por tanto no se toma, B y C se mantienen fijas en 1 mientras que D se mantiene fija en 0, así que nos queda como función del conjunto rojo BCD’.

La funcion final nos queda finalmente:

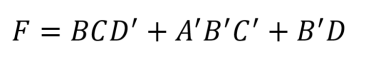
Si lo hubiéramos hecho por miniterminos tendríamos que haber aplicado mucha Álgebra de Boole para llegar a la misma expresión