Concepto de tensión, intensidad, resistencia ...(Parte 2)
Concepto de tensión, intensidad, resistencia ...(Parte 2)
Seguimos… De la ecuación de la Ley de Ohm que vimos anteriormente, podemos despejar los valores de Voltaje y de Resistencia. De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero.

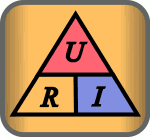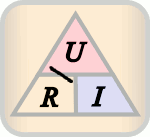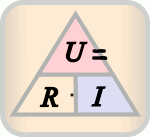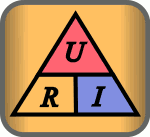
Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso.

En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda.

Tal vez lo veas más claro en la siguiente animación:
Veamos ahora como aplicar la ley en un circuito sencillo:

Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:
I = V / R = 12v / 10Ω = 1,2 Amperios
En un circuito con varias resistencias en serie. Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie. Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación:

En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas. Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias.

En un circuito mixto de resistencias conectadas en serie y en paralelo, aplicaremos lo ya aprendido, pero dividiendo el circuito en subcircuitos de resistencias en función de cómo estén conectadas.

Ahora ya puedes probar con circuitos reales de resistencias si George Simon Ohm estaba en los cierto y los valores que calculemos aplicando su fórmula coinciden con los que midamos. Pero antes, es muy IMPORTANTE tener en cuenta otro factor que completa la definición del circuito y los valores de sus resistencias. Estoy hablando de la Potencia eléctrica consumida en el circuito, que en el caso de las resistencias se transforma íntegramente en calor.
Se dispone de resistencias de 1/8 de watio (W), 1/4 y 1/2, que son las más habituales (se pueden adquirir por lotes completos de valores en Amazon o eBay a precios muy asequibles). Y a partir de ahí, las hay de 1 W, 2 W… hasta donde queramos. Pero a mayor potencia, mayor coste económico y mayor tamaño. Este segundo valor que define a una resistencias, nos indica su máxima capacidad de disipación de potencia en forma de calor sin que llegue a destruirse como la del siguiente video.
“La potencia disipada en un circuito eléctrico es directamente proporcional al voltaje y la corriente que circula.”
Por lo tanto:
W (watios) = V (voltios) x I (amperios)
Y aplicando la Ley de Ohm, podemos integrar la potencia en el siguiente gráfico que facilita la selección de la fórmula que necesitemos aplicar.

Así, por ejemplo, en el circuito más sencillo que analizamos anteriormente con una sola resistencia, su potencia deberá ser de al menos:
W = V x I = 12v x 1,2A = 120 W
Como seguramente no dispongamos de ninguna resistencia de esa potencia, y además sería muy voluminosa, lo mejor será utilizar para las pruebas resistencias de más de 1000 Ω = 1 KiloOhmio = 1 KΩ, de manera que en el ejemplo anterior:
W = V x I = V x V / R = V2 / R = 122 / 1000 = 0,144 W
Utilizando una resistencia de 1 KΩ y al menos 1/4 W (0,250 W), las mediciones y cálculos serían los siguientes:
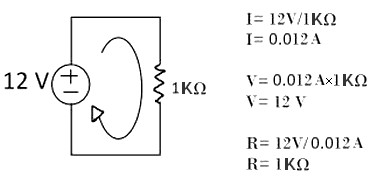
Será necesario realizar ese mismo cálculo de potencia para cada una de las resistencias que empleemos en los circuitos reales que montemos para practicar.
Dependiendo de la utilidad que se le desee dar, existen diferentes tipos o familias de resistencias electrónicas.

Por cierto, que la unidad de resistencia eléctrica sea el Ohmio no es casualidad, recibe este nombre como homenaje a George Simon Ohm.
Fuente: Taller electrónica